17世紀西欧哲学における「数学」の位置づけ(1)
表題について、手始めに、ゴクレニウスの『哲学辞典』Lexicon Philosophicum(1613)における「数学の術・数学」"Mathematicae Artes. Mathemata"の項を参照してみる。どう効いているのかはまだ不明だが、数学をして、"scientia"ではなく"ars"「術」としている点が印象的だ。
ゴクレニウスは、「数学」(Mathemata)は3つの仕方で理解されているという。まず、(1)一般的には、学問・学識・教えとしての「数学」。次に、(2)特殊には幾何学や算術[数論]として、少年たちが第一段階において学ぶ学問のように、ここから着手されるものとしての「数学」。そして、(3)算術や幾何学だけでなく、天文学、光学、音楽、機械学などとしての数学」。
(3)の意義は、数学には算術や幾何学という純粋(pura)数学と、残りの学を含む不純すなわち混合(mixta)数学とがあるように考えられる、ということである。純粋数学は最大限抽象的な(maxime abstractorum)数学で、混合数学は具体的な(concretorum)数学である。このような抽象の度合いに基づく純粋数学と混合数学の分類は、17世紀でも保たれているものである。混合数学は現代でいえば応用数学として理解できるものである。しかし、混合数学はいまだ「応用」という観点からはほど遠く、感覚的質料が混合している学問、数学的部分が観られる学問であって、混合数学と応用数学は同一視されるべきものでもない。
興味深いのは、数学もまた根拠(ratio)ないし原因(causa)をもつ、としている点である。「数学は原理すなわち数学の定理だけでなく、根拠をもまたもっている。われわれは数学の原因を魂に、把握を知解(intelligentia)にもつ」。ここから、ゴクレニウスにおいては、数学が、心的な原因ないし心的な根拠をもつと考えられているように思われる。実際、数学的対象が、抽象という心的過程によって形成されたものであるという、アリストテレス・スコラによる数学の「抽象主義」は、17世紀の数学者・哲学者においても広く保たれている。
数学がしばしば質料(materia)から自由なものとしてありうることが示唆されているが、数学が「抽象」を扱う学であるという理解は、17世紀に共通する数学の理解である。たとえば、ゴクレニウスが、「幾何学は連続的な量における自体的かつ抽象的なものに携わっている」としているようにである。質料を抽象した学問は「数学だけではなく、超自然的なもの(transnaturalia)[すなわち普遍的なものなど]もまた質料から分離され、自由である」とされる。自然学や感覚的なものを扱う学が、数学などに対立するものとして立てられているが、これも当時の標準的な理解であろう。
アリストテレス・スコラ的な学問分類の伝統として特徴的なのは、存在者からの「抽象」の度合いによって、学問が分類されていることである。すなわち、数学の位置づけは、この「抽象」との関係で左右されてきた経緯がある。「存在論」(オントロジー)という哲学用語の初出とされる、同じゴクレニウスの哲学辞典の「質料の抽象」"abstractio materiae"の項を参照してみると、この傾向が引き継がれていることが明らかである。そこで少し脱線することになるかもしれないが、「質料の抽象」の項を確認してみる。
ゴクレニウスは、この項で、「存在論」(Ontologia)を「存在者についての哲学」(philosophia de ENTE)と表現している。存在論と数学は存在者を単一質料および普遍的質料からの抽象によって考察する点で似ているが、存在論が存在者として存在者を考察するのに対し、数学は単に特殊な存在者をしか考察しない。すなわち、抽象の観点から、数学は、単一および普遍的質料からの抽象、つまり、実在的にではなく、限られた考慮に基づいて(すなわち概念的にのみ)捉えられた対象を扱う。
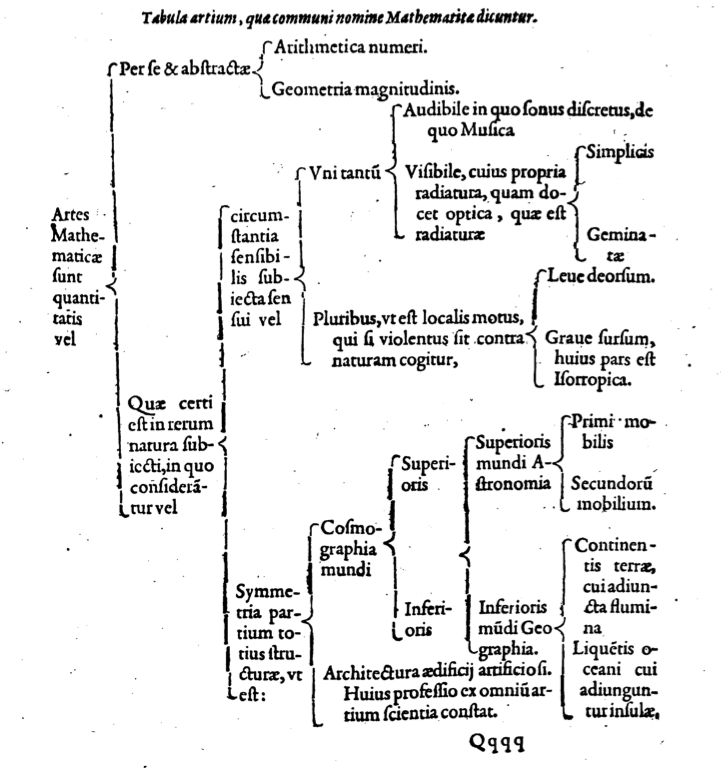
ただし、「数学」は普遍的抽象を扱う純粋数学だけでなく、具体的存在者をも対象として用いる混合数学をも含む、幅広い概念としてもある。そこで、「数学」の項に戻ろう。そこには、「数学」という共通名称で呼ばれる学問の分類表(下図参照)が描かれており、量に関わる多様な学が含まれている。
まず、「数学の術」は「量についての学」とある。これはまず、「自体的かつ抽象的」な学としての数学と、その学において考えられている対象がある基体がもつ事物の自然[本性]のうちにある数学とに分類される。前者は、純粋数学のことで、後者が混合数学のことである。「自体的かつ抽象的」ということでは、基体から抽象された対象を扱うにもかかわらず、その対象を自体的なものとして措定することで成り立っているという、アリストテレス・スコラ的な規定を踏襲しているようである。
純粋数学は、本文にも述べられていたように、「数を扱う算術」と「大きさを扱う幾何学」に分類される。自然的事物を対象とする混合数学は、「感覚の下にある感覚可能なものについての状況」すなわち感覚にかかわる学と、「諸部分の釣合いによる全体の建築術」にかかわる学に分類される。感覚にかかわる学の方には、単一の感覚にかかわる「音楽」や「光学」が配属され、多数の感覚がかかわる学の方には、「局所的運動」についての学などが配属されている。「諸部分の釣合いによる全体の建築術」は、天文学や地理学を下位分類に持つ「宇宙形状誌」と、「人工的な建造物の建築術」とに分類されている。(つづく)